Welcome
Every year, a group of KNU, PNU, OMU, and OU topologists and their academic families and friends is organizing an international conference on knots and related topics alternately at Kyungpook National University, Pusan National University, and Osaka Metropolitan University. The 16th TAPU-KOOK Joint Seminar on Knots and Related Topics and the 18th Graduate Student Workshop on Mathematics will take place at the Department of Mathematics, Kyungpook National University, July 28 - Aug 1, 2025.
Group Photo


A commemorative group photo of the participants of the 16th TAPU-KOOK Joint Seminar and the 18th Graduate Student Workshop on Mathematics, held at Kyungpook National University (July 28 – August 1, 2025).
Invited Speakers
- Hirotaka Akiyoshi (Osaka Metropolitan University, Japan)
- Zhiyun Cheng (Beijing Normal University, China)
- Mustafa Hajij (University of San Francisco, United States)
- Mee Seong Im (Johns Hopkins University, United States)
- Yeonhee Jang (Osaka Metropolitan University, Japan)
- Seiichi Kamada (The University of Osaka, Japan)
- Mikhail Khovanov (Johns Hopkins University, United States)
- Byeorhi Kim (POSTECH, Republic of Korea)
- Jieon Kim (Pusan National University, Republic of Korea)
- Yoosik Kim (Pusan National University, Republic of Korea)
- Sam Nelson (Claremont McKenna College, United States)
- Kodai Wada (Kobe University, Japan)
- Xiao Wang (Jilin University, China)
- Seung Yeop Yang (Kyungpook National University, Republic of Korea)
- Jumpei Yasuda (Osaka Metropolitan University, Japan)
Special Lecture
[KNU G‑LAMP International Seminar]
Date & Time: July 28, 2025 (Mon), 16:30 – 18:00
Location: Room B06, College of Natural Sciences Main Bldg.(#209), Kyungpook National University
Speaker: Mustafa Hajij (University of San Francisco, United States)
Title: Frontiers and Opportunities in Topological Deep Learning
Abstract: In recent years, deep learning has achieved remarkable success across various domains, particularly in tasks involving data structured as regular grids or sequences, such as images and text. However, scientific and real-world data frequently exhibit complex, non-Euclidean structures—including point clouds, meshes, graphs, and higher-order topological spaces—that challenge the assumptions of traditional neural network architectures. Topological Deep Learning (TDL) is an emerging field that extends deep learning methods to handle these rich and intricate data types. By incorporating topological constructs such as simplicial complexes, cell complexes, and hypergraphs, TDL enables the modeling of higher-order relationships, global dependencies, and qualitative spatial properties that are otherwise inaccessible to standard approaches. This talk will explore the foundational ideas behind TDL, the computational and theoretical challenges it presents, and its broad potential to enhance learning in diverse areas—from physics-informed machine learning and neuroscience to social network analysis and beyond.
Organizing Committee
Organizers
- Yongju Bae (Kyungpook National University), Chair
- Sang Youl Lee (Pusan National University)
- Seung Yeop Yang (Kyungpook National University), Preparatory Committee Chair
- Akio Kawauchi (OCAMI)
- Taizo Kanenobu (Osaka Metropolitan University)
- Seiichi Kamada (Osaka University)
- Hirotaka Akiyoshi (Osaka Metropolitan University)
- Yoosik Kim (Pusan National University)
Local Organizers
- Yongju Bae (Kyungpook National University)
- Seung Yeop Yang (Kyungpook National University)
- Byeorhi Kim (POSTECH)
- Jinseok Oh (Kyungpook National University)
- Hongdae Yun (Kyungpook National University)
Support
The 16th TAPU-KOOK Joint Seminar on Knots and Related Topics and The 18th Graduate Student Workshop on Mathematics are supported by the following:








Schedule
Day 0 – July 28
| Time | Speaker | Title | Chair |
|---|---|---|---|
| 14:00 – 16:30 |
Panel Discussion on Knot Theory and Related Topics (Z. Cheng, S. Choi, J. Kim, X. Wang, S. Y. Yang) |
||
| 16:30 – 18:00 | Mustafa Hajij |
[KNU G‑LAMP International Seminar] Frontiers and Opportunities in Topological Deep Learning |
Seung Yeop Yang (Kyungpook National University) |
| 19:00 – | Dinner | ||
Day 1 – July 29
| Time | Speaker | Title | Chair |
|---|---|---|---|
| 09:20 – 09:30 | Yongju Bae (Kyungpook National University) |
Opening Remark | - |
| 09:30 – 10:10 | Mikhail Khovanov (Johns Hopkins University) |
Foams and their applications in link homology and categorification I | Seonmi Choi (Seowon University) |
| 10:10 – 10:50 | Seiichi Kamada (The University of Osaka) |
On commutator identities obtained from doodles on a surface | Yewon Joung (Hanyang University) |
| 10:50 – 11:00 | Break | ||
| 11:00 – 11:30 | Yeonhee Jang (Osaka Metropolitan University) |
Keenness for bridge splitting of links | Seiichi Kamada (The University of Osaka) |
| 11:30 – 12:00 | Mustafa Hajij (University of San Francisco) |
Cellular Transformer: A Topological Deep Learning Framework for Molecular Understanding | Yeonhee Jang (Osaka Metropolitan University) |
| 12:00 – 13:30 | Lunch | ||
| 13:30 – 14:00 | Zhiyun Cheng (Beijing Normal University) |
Invariants for knots in $\Sigma_g\times I$ and knots in $\Sigma_g\times S^1$ | Mustafa Hajij (University of San Francisco) |
| 14:00 – 14:30 | Jumpei Yasuda (Osaka Metropolitan University) |
2-plat 2-knots and their double branched covers | Zhiyun Cheng (Beijing Normal University) |
| 14:30 – 14:40 | Break | ||
| 14:40 – 14:50 | Seung Yeop Yang (Kyungpook National University) |
Opening Remark | - |
|
14:50 – 15:50 (GSW-Part1) |
Katsunori Arai (The University of Osaka) |
An infinite family of pairs of spatial surfaces | Yoosik Kim (Pusan National University) |
|
Sanghoon Park (Pusan National University) |
Introduction to triple point number of surface-links | ||
|
Ryoya Kai (Osaka Metropolitan University) |
An example of a family of quandle extensions | ||
|
Daesick Ryu (Kyungpook National University) |
Synergistic combination between CFD and AI for heat transfer optimization in hybrid nanofluids system | ||
| 15:50 – 16:00 | Break | ||
| 16:00 – 17:00 (GSW-Part2) |
Jinichiro Tanaka (Osaka Metropolitan University) |
On the Bott--Chern and Aeppli cohomology of 2-dimensional theta toroidal groups. | Yeonhee Jang (Osaka Metropolitan University) |
| Joy Nana Okogun-Odompley (Pusan National University) |
Mathematical Modelling of Malaria: Mother-to-Child Transmission and Dragonfly Predation | ||
| Yuri Yamashita (Osaka Metropolitan University) |
Geometry of left-invariant pseudo-Riemannian metrics on Lie groups and closed orbit spaces | ||
| Galmandakh Tsog-Ochir (Kyungpook National University) |
Projective Dimensional Properties of the Hurwitz Module | ||
| 17:00 – 17:10 | Break | ||
| 17:10 – 18:10 (GSW-Part3) |
Haruchika Tsuno (The University of Osaka) |
2-dimensional braids over $P^2_-$ of degree two | Jieon Kim (Pusan National University) |
| Amare Tezera Dessie (Pusan National University) |
Fractional-Order Modeling of HIV-Tuberculosis (TB) Co-infection with TB Prophylaxis in South Korea | ||
| Yangyang Zhang (Osaka Metropolitan University) |
On example of nef,big and non-semipositive line bundles | ||
| Sangsoo Lee (Kyungpook National University) |
Introduction to Colored Jones Polynomial | ||
| 18:10 – | Dinner | ||
Day 2 – July 30
| Time | Speaker | Title | Chair |
|---|---|---|---|
| 09:30 – 10:10 | Mikhail Khovanov (Johns Hopkins University) |
Foams and their applications in link homology and categorification II | Seonmi Choi (Seowon University) |
| 10:10 – 10:50 | Sam Nelson (Claremont McKenna College) |
Quiver Categorification of Homset Invariants | Sang Youl Lee (Pusan National University) |
| 10:50 – 11:00 | Break | ||
| 11:00 – 11:30 | Mee Seong Im (Johns Hopkins University) |
Sah-Arnoux-Fathi invariants, algebraic K-theory and foam cobordisms | Sam Nelson (Claremont McKenna College) |
| 11:30 – 12:00 | Xiao Wang (Jilin University) |
On computation of the Kauffman bracket skein module | Mee Seong Im (Johns Hopkins University) |
| 12:00 – 13:30 | Lunch | ||
| 13:30 – 14:00 | Byeorhi Kim (POSTECH) |
On topological mapping class groups of 4-Manifolds via the Dax Invariant | Xiao Wang (Jilin University) |
| 14:00 – 14:30 | Seung Yeop Yang (Kyungpook National University) |
On the Betti numbers of the set-theoretic Yang–Baxter cohomology of Alexander biquandles | Byeorhi Kim (POSTECH) |
| 14:30 – 14:40 | Break | ||
| 14:40 – 15:40 (GSW-Part4) |
Fumika Mizoguchi (Osaka Metropolitan University) |
Solvable Lie algebras obtained by quivers and Einstein metrics | Jumpei Yasuda (Osaka Metropolitan University) |
| Miji Kim (Pusan National University) |
Deep Learning-Based Forecasting of Sea Temperature in the East Sea Using 2D ConvLSTM | ||
| Hina Kitayama (Osaka Metropolitan University) |
Nilpotent Lie algebras obtained by quivers with cycles and Algebraic Ricci solitons | ||
| Jaewoo Hwang (Kyungpook National University) |
Investigation on inflammation and remission times in atopic dermatitis system | ||
| 15:40 – 15:50 | Break | ||
| 15:50 – 16:50 (GSW-Part5) |
Ryosuke Miki (The University of Osaka) |
A quandle which is related to the relative homotopy group of a knotted surface exterior with a handle decomposition | Dongsoo Lee (KAIST) |
| Meiling Li (Pusan National University) |
Comparative causal inference methods for environmental factor of influenza A and B outbreak in Korea | ||
| Kazuki Sato (Osaka Metropolitan University) |
One-dimensional boundary blow-up problem with an exponential nonlinearity | ||
| Jinyoung Heo (Kyungpook National University) |
A survey on geometric realizations of Khovanov homology of Pretzel links | ||
| 16:50 – 17:00 | Break | ||
| 17:00 – 18:00 (GSW-Part6) |
Ryohei Mashino (Osaka Metropolitan University) |
Asymptotic stability for a linear difference equation with off-diagonal delays | Byeorhi Kim (POSTECH) |
| Hyungu Lee (Kyungpook National University) |
Optimized Weight Initialization on the Stiefel Manifold for Deep ReLU Networks | ||
| Haruko Matsuzawa (Osaka Metropolitan University) |
Geometric McKay Correspondence | ||
| Junseok Moon (Kyungpook National University) |
A survey on triple point numbers of Fox's example 15 | ||
| 18:00 – 18:10 | Group Photo | ||
| 18:10 – | Banquet | ||
Day 3 – July 31
| Time | Speaker | Title | Chair |
|---|---|---|---|
| 09:30 – 10:10 | Mikhail Khovanov (Johns Hopkins University) |
Foams and their applications in link homology and categorification III | Seonmi Choi (Seowon University) |
| 10:10 – 10:20 | Break | ||
| 10:20 – 10:50 | Kodai Wada (Kobe University) |
The intersection polynomials of a long virtual knot | Seung Yeop Yang (Kyungpook National University) |
| 10:50 – 11:20 | Yoosik Kim (Pusan National University) |
Topology of fibers of bending systems in 3D polygon spaces | Kodai Wada (Kobe University) |
| 11:20 – 11:30 | Break | ||
| 11:30 – 12:00 | Jieon Kim (Pusan National University) |
Immersed surface-links presented by a triangle chs-graph | Yoosik Kim (Pusan National University) |
| 12:00 – 12:30 | Hirotaka Akiyoshi (Osaka Metropolitan University) |
Finding Dirichlet domains, II | Jieon Kim (Pusan National University) |
| 12:30 – 12:40 | Group Photo | ||
| 12:40 – 12:50 | Seung Yeop Yang (Kyungpook National University) |
GSW Awards Ceremony | - |
| 12:50 – 13:00 | Seung Yeop Yang (Kyungpook National University) |
Closing Remark | - |
| 13:00 –14:20 | Lunch | ||
| 14:20 –18:10 | Free discission | ||
| 18:10 – | Dinner | ||
Day 4 – August 1
| Time | Speaker | Title | Chair |
|---|---|---|---|
| 09:30 – 11:30 |
Panel Discussion on Knot Theory and Related Topics (Z. Cheng, Y. Jang, Y. Kim, X. Wang, S. Y. Yang) |
||
Abstracts
The 16th TAPU-KOOK Joint Seminar on Knots and Related Topics
Title : Finding Dirichlet domains, II
Speaker : Hirotaka Akiyoshi (Osaka Metropolitan University)
Abstract : In my talk at The 14th TAPU-KOOK Joint Seminar on Knots and Related Topics, I introduced a project involving numerical experiments whose aim is to determine the Dirichlet domains for hyperbolic manifolds. This talk is a continuation of that work, focusing on new developments and applications. We study Dirichlet domains for certain hyperbolic structures on the closed orientable surface of genus 2, and for every point on the surface we numerically determine the Dirichlet domain with respect to the point. Based on the result, we also discuss the diameters of the surfaces.
Title : Invariants for knots in $\Sigma_g\times I$ and knots in $\Sigma_g\times S^1$
Speaker : Zhiyun Cheng (Beijing Normal University)
Abstract : In this talk, I will discuss how to use index and quandle to define knot invariants for knots in 3-manifolds mentioned in the title. This talk is based on joint work with Hongzhu Gao.
Title : Cellular Transformer: A Topological Deep Learning Framework for Molecular Understanding
Speaker : Mustafa Hajij (University of San Francisco)
Abstract : We introduce the Cellular Transformer, a novel topological deep learning (TDL) framework that generalizes graph transformers to operate on regular cell complexes enabling a deeper and more expressive modeling of higher-order molecular structures. Accurately representing complex biomolecules remains a central challenge in computational chemistry, largely due to the intricate interplay between geometry and topology. While traditional graph neural networks (GNNs) and graph transformers have made strides, they often fall short in handling higher-order structures such as fused rings, aromatic systems, and nested cycles. These limitations arise from their reliance on node-edge representations and often require heuristics like virtual nodes, graph rewiring, or domain-specific encodings. Our approach is principled and native: CT directly leverages the structure of cell complexes to encode topological features—capturing loops, cliques, and ring-level motifs in a mathematically grounded manner. To support this, we introduce the augmented molecular cell complex, a richer molecular representation that retains essential ring- and bond-level context, critical for tasks in drug discovery and chemical property prediction. Extensive evaluations on MoleculeNet and newly constructed cell-complex datasets demonstrate that CT consistently outperforms standard GNNs and graph transformers, while avoiding the need for domain-specific augmentation. Remarkably, our model achieves this without relying on virtual nodes, structural encodings, or rewiring techniques, illustrating the power of topologically informed attention mechanisms in capturing subtle and global molecular interactions.
Title : Sah-Arnoux-Fathi invariants, algebraic K-theory and foam cobordisms
Speaker : Mee Seong Im (Johns Hopkins University)
Abstract : I will introduce scissor congruence and algebraic K-theory and how they are related to cobordism groups of foams in various dimensions. The former is joint with Mikhail Khovanov while the latter is joint with David Gepner, Mikhail Khovanov, and Nitu Kitchloo.
Title : Keenness for bridge splitting of links
Speaker : Yeonhee Jang (Osaka Metropolitan University)
Abstract : Hempel distance for a bridge splitting of a link is defined to be the distance in the curve complex of the bridge surface between the two subcomplexes corresponding to the two parts of the bridge splitting. We say that a bridge splitting is keen if the pair of vertices in the curve complex realizing the Hempel distance is unique, and is weakly keen if the set of the pairs of vertices realizing the Hempel distance is finite. In this talk, we review our result on the existence of keen bridge splttings and give some observations on weakly keen bridge splittings.
Title : On commutator identities obtained from doodles on a surface
Speaker : Seiichi Kamada (The University of Osaka)
Abstract : R. Fenn and P. Taylor introduced the notion of a doodle and showed that a doodle diagram, which is a collection of curves on the 2-sphere, induces an identity among commutators in a free group. This idea was observed more closely in a paper by A. Bartholomew, R. Fenn, N. Kamada and S. Kamada [JKTR 31 (2022)]. On the other hand, the notion of a doodle on the sphere can be extended to any surface with positive genus (cf.[JKTR 27 (2018)]). We discuss commutator identities obtained from doodles on a surface. It is a part of a project by A. Bartholomew, R. Fenn, N. Kamada and S. Kamada.
Title : Foams and their applications in link homology and categorification
Speaker : Mikhail Khovanov (Johns Hopkins University)
Abstract : In this series of talks we’ll introduce foams and their evaluation due to Robert and Wagner given by a version of state sum model in three dimensions that counts embedded surfaces. In the special 3-color case this model relates to the Four-Color Theorem and it also gives rise to a categorification of the quantum SL(3) invariant. We also explain how it works for N colors and discuss its applications, including to a 3-dimensional interpretation of the category of Soergel bimodules.
Title : On topological mapping class groups of 4-Manifolds via the Dax Invariant
Speaker : Byeorhi Kim (POSTECH)
In this talk, we study the topological mapping class group of a 4-manifold $M = \#^r_\partial (S^1 \times D^3) \#_\partial (S^2 \times D^2)$ formed as a boundary connected sum. Motivated by Gabai’s recent results on the failure of isotopy for homotopic 3-balls, we reinterpret such phenomena in terms of a topological Dax invariant, introduced in our previous work. As a result, we show that the topological Dax invariant detects nontrivial mapping classes that are homotopically trivial.
Title : Immersed surface-links presented by a triangle chs-graph
Speaker : Jieon Kim (Pusan National University)
An immersed surface-link is a surface smoothly immersed in $\Bbb R^4$ such that the multiple points are transverse double points. Such a surface can be represented by a planar 4-valent graph embedding with the vertices of three types. By considering the dual graph of this diagram, one can construct another presentation, called a chs-graph. In this talk, we focus especially on the case where the chs-graph takes the form of a triangular-shaped graph.
Title : Topology of fibers of bending systems in 3D polygon spaces
Speaker : Yoosik Kim (Pusan National University)
Abstract : In this talk, we discuss polygon spaces in $R^3$, which can be regarded as moduli spaces of discretized knots with fixed edge lengths. We introduce a symplectic-geometric method for studying this polygon space, and then explain how the topology of certain subset consisting of degenerate knots can be understood via the Gelfand–MacPherson correspondence.
Title : Quiver Categorification of Homset Invariants
Speaker : Sam Nelson (Claremont McKenna College)
Abstract : The quandle coloring quiver and similar constructions provide a way of turning homset- based invariants into categories. In this talk we will examine this phenomenon with several examples.
Title : The intersection polynomials of a long virtual knot
Speaker : Kodai Wada (Kobe University)
Abstract : In this talk, we introduce twelve kinds of polynomial invariants of a long virtual knot called the intersection polynomials, and establish some fundamental properties of them such as their behavior under orientation-reversal/mirror-reflection, and additivity under concatenation product. Moreover, we provide a characterization of each of the intersection polynomials. We also introduce two kinds of supporting genera of a long virtual knot as a new topological property, and give a relationship between these supporting genera and the intersection polynomials. This is joint work with Takuji Nakamura, Yasutaka Nakanishi and Shin Satoh.
Title : On computation of the Kauffman bracket skein module
Speaker : Xiao Wang (Jilin University)
Abstract : Kauffman bracket skein module is an important object in low dimensional topology, while its computation is in general difficult. In this talk, we will focus on the Kauffman bracket skein module of $(S^1 \times S^2)\#(S^1 \times S^2)$, and show its structure does not split into free and torsion parts. Then we extend the method to the Kauffman bracket skein module of certain three manifolds obtained from genus two handlebody by attaching 2 and 3-handles.
Title : On the Betti numbers of the set-theoretic Yang–Baxter cohomology of Alexander biquandles
Speaker : Seung Yeop Yang (Kyungpook National University, Republic of Korea)
Abstract : The ranks of the homology groups of finite quandles were established by Etingof and Graña. Subsequently, Wang and Yang extended this result to the case of finite cyclic biquandles. The independence of the two coordinates in the Yang–Baxter operators for quandles and cyclic biquandles leads to relatively simple algebraic structures, whereas the interdependence in Alexander biquandles results in greater difficulty in analyzing their homology groups. In this talk, we study upper and lower bounds for the Betti numbers of the set-theoretic Yang–Baxter cohomology groups of finite Alexander biquandles.
Title : 2-plat 2-knots and their double branched covers
Speaker : Jumpei Yasuda (Osaka Metropolitan University)
Abstract : A 2-knot is a 2-sphere smoothly embedded in the 4-sphere. In this talk, we introduce a new family of 2-knots, called 2-plat 2-knots, which are higher-dimensional analogues of 2-bridge knots. These 2-knots admit normal forms parametrized by rational numbers. We provide a formula for their Alexander polynomials and determine their double branched covers.
The 18th Graduate Student Workshop on Mathematics
Title : An infinite family of pairs of spatial surfaces
Speaker : Katsunori Arai (The University of Osaka)
Abstract : A spatial surface is a compact surface embedded in the 3-sphere. In this talk, we assume that spatial surfaces are oriented and that each connected component is neither a 2-disk nor a closed surface. Such surfaces can be presented by diagrams of spatial trivalent graphs and Reidemeister type theorem holds. A rack is a set equipped with a binary operation satisfying axioms motivated by two of the three Reidemeister moves in knot theory. A multiple group rack (MGR) is a rack defined on a disjoint union of groups, satisfying conditions corresponding to Reidemeister moves for spatial surfaces. Using MGRs, we can construct invariants of spatial surfaces up to ambient isotopy. In this talk, we provide an infinite family of pairs of spatial surfaces which have the same boundary, isomorphic fundamental groups of their complements, and Seifert matrices that are unimodular congruent. We show that the spatial surfaces in each pair of the family are not ambiently isotopic by distinguishing them using invariants derived from MGRs.
Title : Fractional-Order Modeling of HIV-Tuberculosis (TB) Co-infection with TB Prophylaxis in South Korea
Speaker : Amare Tezera Dessie (Pusan National University)
Abstract : Tuberculosis (TB) remains a significant public health challenge in South Korea, while HIV prevalence is relatively low. This ongoing study develops a fractional-order differential equation model tailored to the South Korean epidemiological context to investigate the dynamics of HIV-TB co-infection. The model incorporates TB treatment strategies, including Isoniazid Preventive Therapy (IPT) administered to individuals at risk of TB before infection to prevent progression from latent to active disease, and standard TB treatment regimens for active cases. Additionally, it quantifies the impact of Antiretroviral Therapy (ART) for HIV management in co-infected individuals. Fractional-order modeling is employed to capture memory effects and non-local interactions, providing a more accurate representation of complex biological and epidemiological processes compared to traditional integer-order models. Through numerical simulations, I assess the combined effectiveness of pre-infection IPT, postinfection TB treatment, and ART in reducing TB transmission, reactivation, and HIV progression. The study evaluates the stability and sensitivity of co-infection dynamics under various treatment scenarios. The fractional-order approach enhances predictive accuracy for treatment outcomes, offering critical insights for optimizing integrated TBHIV intervention strategies in South Korea, with a focus on HIV control.
Title : A survey on geometric realizations of Khovanov homology of Pretzel links
Speaker : Jinyoung Heo (Kyungpook National University)
Abstract : Khovanov homology, introduced by Mikhail Khovanov in 2000, is a categorification of the Jones polynomial and provides a powerful invariant of knots and links. In 2018, J. González-Meneses, P. M. G. Manchón, and M. Silvero gave a geometric realization of the extreme Khovanov homology. In 2020, J. H. Przytycki and M. Silvero conjectured that the extreme Khovanov homology of any link is torsion-free. In 2025, J. Oh et al. partially showed that the conjecture holds for certain families of $3$-strand pretzel links by using their geometric realizations of the extreme Khovanov homology. In this talk, we review the geometric realization of the extreme Khovanov homology for $3$-strand pretzel links.
Title : Investigation on inflammation and remission times in atopic dermatitis system
Speaker : Jaewoo Hwang (Kyungpook National University)
Abstract : Atopic dermatitis (AD) is a chronic skin disease characterized by recurrent cycles of inflammatory response and remission, depending on the patient’s skin permeability ($\kappa_P$) and immune response ($\alpha_I$). Although it is not life-threatening, AD significantly impairs patients’ quality of life due to persistent or frequently recurring symptoms. In this talk, we discuss mathematical analysis of inflammation time ($\tau_I$) and remission time ($\tau_R$) in the AD system. We investigate how $\kappa_P$ and $\alpha_I$ affect $\tau_R$ and $\tau_I$ in cases of mild and serious oscillation, respectively. Especially, we highlight two interesting dynamical behaviors for these measurements: the logarithmic scaling law in $\tau_R$ and the phase transition of $\tau_R$ and $\tau_I$.
Title : An example of a family of quandle extensions
Speaker : Ryoya Kai (Osaka Metropolitan University)
Abstract : A quandle extension is a surjective quandle homomorphism whose fibers have the same cardinality. This notion is a generalization of a quandle 2-cocycle, and plays an important role in knot theory. However, it is difficult to construct quandle extensions in general. One of the simplest non-trivial examples is the extension from the octahedral quandle with type 4 to the dihedral quandle with degree 3. This example can be understood using natural projection from the 2-sphere to the projective plane. In this talk, we generalize this extension, and give a new infinite family of quandle extensions by using the geometry of oriented 2-plane Grassmannians, which is a generalization of the 2-sphere. In addition, we provide some properties of these extensions. This talk is based on a joint work with Hiroshi Tamaru (Osaka Metropolitan University).
Title : Deep Learning-Based Forecasting of Sea Temperature in the East Sea Using 2D ConvLSTM
Speaker : Miji Kim (Pusan National University)
Abstract : This study aims to predict sea temperature and salinity in the East Sea using a data-driven deep learning model, and to explore the potential for predicting sound speed based on these variables. The data used in this study is HYCOM ocean reanalysis data from May 1 to October 31, 2020, with a 3-hour interval. The study area is set between latitudes 36.3°–37.3° and longitudes 129.4°–130.2°. The model applied is based on a 2D ConvLSTM architecture, with a spatial resolution maintained at a 25×10 grid. Areas containing missing values (NaNs) were masked to prevent them from affecting the learning process. Each input sequence consists of 56 past time steps, and the model is designed to predict the subsequent 8 time steps. In the initial experiments, the prediction results for a specific date were compared with actual observations to visualize the errors. The spatial prediction performance of the model was evaluated using error maps between the true and predicted values. Additionally, attention weight variations were introduced, and hyperparameter tuning was performed to enhance prediction performance. This study is expected to provide foundational data for future precise marine environmental forecasting in the East Sea and for applications in underwater acoustic communication.
Title : Nilpotent Lie algebras obtained by quivers with cycles and Algebraic Ricci solitons
Speaker : Hina Kitayama (Osaka Metropolitan University)
Abstract : A quiver is a directed graph represented by edges and vertices that allows multiple edges and loops. Recently, Mizoguchi-Tamaru developed a method for constructing nilpotent Lie algebra from quivers, and proved the nilpotent Lie algebras obtained from a quiver without cycles always admits an algebraic Ricci soliton. In this talk, I will first introduce a method for constructing nilpotent Lie algebras from quivers with cycles, which is an extension of the method from previous research. Then, I will present the results we have obtained regarding the conditions for the simply connected Lie groups corresponding to the obtained nilpotent Lie algebras to admit left-invariant Ricci soliton Riemannian metrics.
Title : Optimized Weight Initialization on the Stiefel Manifold for Deep ReLU Networks
Speaker : Hyungu Lee (Kyungpook National University)
Abstract : Weight initialization critically affects training efficiency and convergence in deep nets. Popular schemes like Xavier, He, and standard orthogonal methods maintain signal variance and stabilize gradients, but they don’t solve the dying ReLU issue inherent to ReLU activations. We introduce a Stiefel-manifold–based orthogonal initialization tailored for deep ReLU networks, which generates weights that preserve orthogonality, retain the input mean, and bias activations into the positive orthant. Via theoretical analysis and empirical validation, we show this approach stabilizes gradient flow, preserves key input statistics, and effectively mitigates dying ReLUs. As a result, our method boosts both training speed and robustness in deep ReLU–based architectures.
Title : Introduction to Colored Jones Polynomial
Speaker : Sangsoo Lee (Kyungpook National University)
Abstract : The colored Jones polynomial is a central invariant in low‑dimensional topology, capturing deep relationships between knot theory, quantum groups, and 3‑manifold invariants. In this survey, we introduce its definition via right‑quantum matrices and demonstrate how to compute it through explicit examples.
Title : Comparative causal inference methods for environmental factor of influenza A and B outbreak in Korea
Speaker : Meiling Li (Pusan National University)
Abstract : Influenza is an acute respiratory infectious disease of global importance, and among them, types A and B are the most widely spread virus types in the human population. Both viruses are prevalent every year, but they differ in the timing, duration, and severity of the epidemic. Therefore, understanding the environmental factors that affect types A and B influenza is important for increasing understanding of the disease and establishing effective preventive measures. In this study, we analyzed the impact of environmental factors on Influenza A, B, and ALL by utilizing various causal inference methodologies such as Granger Causality (GC), Convergent Cross Mapping (CCM), Partial Cross Mapping (PCM), and General Model-based Causal Inference Method (GOBI). Based on the causal relationships derived from each methodology, we constructed seq2seq prediction models in the direction of environmental factors as causes and influenza as outcomes, and we evaluated the importance of environmental factors through prediction performance. To this end, we introduced the Causal Important Score (CIS), which compares the prediction errors between models that use all variables and only important factors. The results of the analysis showed that GC was effective for type A, CCM for type B, and GOBI for overall influenza. NO₂, O₃, and SO₂ were common important factors in all types, while CO and PM10 were important only in A and B. The temperature index had a clear causal effect in types A and B, with type A becoming more prevalent when temperatures rise in winter, and type B becoming more prevalent in cold spring. Average humidity was important in all types, and wind speed showed a negative causal effect.
Title : Asymptotic stability for a linear difference equation with off-diagonal delays
Speaker : Ryohei Mashino (Osaka Metropolitan University)
Abstract : The zero solution of a difference equation is called asymptotically stable if any solution converges to 0. The effect of delays on the asymptotic stability of the zero solution is fully understood only in some linear equations and is generally unsolved. In this study, we consider a linear difference equation with delays in the off-diagonal terms, and establish the explicit necessary and sufficient conditions for the zero solution to be asymptotically stable in terms of the coefficients and delay parameters.
Title : Geometric McKay Correspondence
Speaker : Haruko Matsuzawa (Osaka Metropolitan University)
Abstract : I will introduce what is so-called the geometric McKay correspondence. This is a correspondence between irreducible representations of a finite subgroup $G$ of $\it{SL}(2, \mathbb{C})$ and the exceptional divisors of the minimal resolution of the quotient singularity $C^2/G$. This phenomenon, relationship between representation theory and algebraic geometry, is based on the original McKay correspondence observed by John McKay in 1979, and it has been a subject of research from various perspectives up to the present day.
Title : A quandle which is related to the relative homotopy group of a knotted surface exterior with a handle decomposition
Speaker : Ryosuke Miki (The University of Osaka)
Abstract : It is well known a handle decomposition of the exterior of a knotted surface can be read from its banded link presentation. Using this fact, J.F. Martins established a method to compute the relative homotopy group of a knotted surface exterior. Moreover, it is well known that the quandle is a very powerful tool in knot theory. In this talk, I will introduce a quandle related to the relative homotopy group of a knotted surface exterior with a handle decomposition read from its banded link presentation, and introduce a quandle crossed module involving this quandle.
Title : Solvable Lie algebras obtained by quivers and Einstein metrics
Speaker : Fumika Mizoguchi (Osaka Metropolitan University)
Abstract : Nilpotent and solvable Lie groups are interesting subjects in the study of special left-invariant geometric structures on Lie groups. In our previous work, we constructed nilpotent Lie algebras from finite quivers without cycles by utilizing the concept of paths within quivers, and we proved that the corresponding simply-connected Lie groups admit Ricci solitons. In this talk, we extend our approach by constructing solvable Lie algebras from finite quivers without cycles, adding vertices as paths of length zero. We prove that if a quiver is an oriented multi-tree, the solvable Lie group obtained by this quiver admits a left-invariant metric, which is isometric to the direct product of a flat metric and an Einstein metric.
Title : A survey on triple point numbers of Fox's example 15
Speaker : Junseok Moon (Kyungpook National University)
Abstract : The triple point number \(t(F)\) is the minimal number of triple points in all diagrams of a surface knot. T. Yajima proved that an $2$-knot has triple point number zero if and only if it is of ribbon type. S. Satoh showed that there is no $2$-knot whose triple point number is equal to one, two, or three. In 2004, A. Shima and S. Satoh gave a lower bound of the triple point number in terms of a quandle cocycle invariant with respect to the 3‑dihedral quandle and proved that the 2‑twist‑spun trefoil has triple point number four. In this talk, we study \(t(F)\) for Fox's example 15.
Title : Mathematical Modelling of Malaria: Mother-to-Child Transmission and Dragonfly Predation
Speaker : Joy Nana Okogun-Odompley (Pusan National University)
Abstract : Malaria remains a major public health concern, particularly in Sub-Saharan Africa, where it causes significant morbidity and mortality. While traditional vector control methods such as insecticide-treated nets and indoor spraying have had positive impacts, the increasing resistance of mosquito populations to chemical interventions calls for sustainable and ecologically viable alternatives. This study proposes a compartmental model for malaria transmission that incorporates dragonfly predation as a natural mosquito control mechanism. The model extends classical SIR-type frameworks by including exposed compartments for both human and mosquito populations and introduces a dragonfly predation term into the mosquito dynamics. Dragonflies are effective predators of mosquitoes at both larval and adult stages, and their integration into the model represents a biologically grounded approach to reducing vector populations.
Title : Introduction to triple point number of surface-links
Speaker : Sanghoon Park (Pusan National University)
Abstract : A surface-link is a smoothly embedded closed surface in $\mathbb{R}^4$. As knot diagrams in classical knot theory, we consider projecting this surface one dimension down. The triple point number corresponds concept of crossing number in knot diagram. It is one of the invariants of surface-links. In this talk, we review the representation of surface-links and discuss how to find upper and lower bounds for computing triple point numbers.
Title : Synergistic combination between CFD and AI for heat transfer optimization in hybrid nanofluids system
Speaker : Daesick Ryu (Kyungpook National University)
Abstract : This research explores the synergistic combination of computational fluid dynamics (CFD) and artificial intelligence (AI) to optimize heat transfer in hybrid nanofluids systems. The study focuses on the magneto-bioconvective behavior of hybrid nanofluids containing oxytactic microorganisms within an inclined porous annulus. The governing equations are solved numerically, revealing complex interactions among multiple parameters that influence heat and mass transfer. To address the computational challenges, a CFD-ANN-GA approach is proposed, integrating artificial neural networks (ANN) and genetic algorithms (GA) to identify optimal parameter settings efficiently. The ANN model, trained on a dataset of 212 CFD simulations, achieved high performance in predicting Nusselt number and Sherwood number. Sensitivity analysis further elucidated the influence of various parameters on thermal transport, providing valuable insights for enhancing heat transfer efficiency in hybrid nanofluids systems. This research demonstrates the potential of combining CFD and AI to advance thermal management technologies.
Title : One-dimensional boundary blow-up problem with an exponential nonlinearity
Speaker : Kazuki Sato (Osaka Metropolitan University)
Abstract : "A boundary blow-up problem" refers to a boundary value problem in which the solution diverges to infinity near the boundary of the domain. It is known that such problems admit a solution when the nonlinear term satisfies the Keller–Osserman condition. In this talk, we consider a one-dimensional boundary blow-up problem with an exponential nonlinearity. We show that the problem admits a unique solution, which can be obtained in an explicit form. This is joint work with Futoshi Takahashi.
Title : Projective Dimensional Properties of the Hurwitz Module
Speaker : Galmandakh Tsog-Ochir (Kyungpook National University)
Abstract : Suppose $R$ be a commutative ring with identity, let $hR$ be the well-known Hurwitz polynomial ring over $R$ and let $M$ be an $R$-module. Then we construct the module over $hR$ as $HM=hR\otimes_R M$, which we call the Hurwitz module. In this talk, we compared Hurwtiz module with usual polynomial module ($R[x]$-module), and investigated under what condition the Hurwitz modules and the $R[x]$-modules would be isomorphic with each other. Furthermore, we explored some properties on projective dimension of the Hurwitz module $HM$.
Title : 2-dimensional braids over $P^2_-$ of degree two
Speaker : Haruchika Tsuno (The University of Osaka)
Abstract : A 2-dimensional braid over $P^2_-$ is an analogue of a closed 2-dimensional braid, introduced by O. Viro and S. Kamada. It is a branched covering surface embedded in a regular neighborhood of a standard projective plane $P^2_-$ in $\mathbf{R}^4$, regarded as a disk bundle over $P^2_-$. In this talk, we will introduce the chart presentation of 2-dimensional braids over $P^2_-$, a method to represent them by graphs, and classify 2-dimensional braids over $P^2_-$ of degree two by the chart presentation.
Title : On the Bott--Chern and Aeppli cohomology of $2$-dimensional theta toroidal groups.
Speaker : Jinichiro Tanaka (Osaka Metropolitan University)
Abstract : A toroidal group $X$ is a connected complex abelian Lie group without non-constant holomorphic functions, and can be regarded as a generalization of a complex torus. If all the Dolbeault cohomologies $H^{p,q}(X, \mathcal{O}_X)$ are finite-dimensional, it is called a theta toroidal group. Umeno identified the de Rham cohomology $H^k_{DR}(X,\mathbb{C})$, and demonstrated the Hodge decomposition $H^k_{DR}(X,\mathbb{C}) = \bigoplus_{p+q=k}H^{p,q}(X, \mathcal{O}_X)$ for every theta toroidal group $X$. Thus, theta toroidal groups resemble complex tori as compact complex manifolds. Then we focus on Bott--Chern and Aeppli cohomology, which play important roles in the study of compact complex manifolds. In this talk, we will observe the Bott--Chern and Aeppli cohomology of non-compact $2$-dimensional theta toroidal groups.
Title : Geometry of left-invariant pseudo-Riemannian metrics on Lie groups and closed orbit spaces
Speaker : Yuri Yamashita (Osaka Metropolitan University)
Abstract : In geometry, the classification of distinguished metrics is an important issue. In this research, we consider distiguished left-invariant pseudo-Riemannian metrics on Lie groups. It is a natural and important problem to determine whether a given Lie group G admits some distinguished left-invariant pseudo-Riemannian metrics or not. For a given Lie group, there is a natural group action on the space of left-invariant pseudo-Riemannian metrics by the scalar multiplication and automorphisms. The orbit space of this group action is called the moduli space. However, in general, the moduli space is not Hausdorff and is complex. Therefore, in this research, we particularly focus on the closed orbit space among these orbit spaces. In this talk, we introduce that it is sufficient to consider metrics only on the closed orbit space to study existence and nonexistance of distinguished metrics. Additionally, we have determined the closed orbit space for some Lie groups. This result suggests a relationship between distinguished points in the closed orbit space and distinguished metrics.
Title : On example of nef,big and non-semipositive line bundles
Speaker : Yangyang Zhang (Osaka Metropolitan University)
Abstract : Kodaira's embedding theorem states that if a compact $K\ddot{a}hler$ manifold $X$ admits a positive line bundle $L$, then $X$ can be embedded into projective space. In other words, $L$ is ample. From this perspective, the algebraic-geometric properties of being nef and big are considered generalizations of ampleness. Therefore, in version of Kodaira's theorem, it is natural to expect that such line bundles might also be semipositive. Based on this observation, I have conducted research starting from the question: Does there exist a line bundle that is nef and big but not semipositive? In the case of dimension one, it is known that every nef and big line bundle is positive. However, in what might be seen as a “surprising” result, Dano Kim constructed an explicit example in dimension three or higher of a line bundle that is nef and big but not semipositive. This naturally shifts attention to the two-dimensional case. Filip and Tosatti proposed the following conjecture: The line bundle in Grauert's example is expected to be nef and big but not semipositive. Based on this conjecture, Koike proved that the line bundle in a modified version of Grauert's example is indeed nef and big but not semipositive. The goal of this talk is to prove that Filip and Tosatti's conjecture is true by analyzing the structure of the original Grauert example and using the tool of the first obstruction class.
Participants
| No. | Name | Affiliation |
|---|---|---|
| 1 | Hirotaka Akiyoshi | Osaka Metropolitan University, Japan |
| 2 | Katsunori Arai | The University of Osaka, Japan |
| 3 | Hyungtae Baek | Kyungpook National University, Republic of Korea |
| 4 | Yongju Bae | Kyungpook National University, Republic of Korea |
| 5 | Seonghyeon Byeon | Kyungpook National University, Republic of Korea |
| 6 | Zhiyun Cheng | Beijing Normal University, China |
| 7 | Eunchan Cho | Korea Science Academy of KAIST, Republic of Korea |
| 8 | Hyukjae Choi | Korea Science Academy of KAIST, Republic of Korea |
| 9 | Seonmi Choi | Seowon University, Republic of Korea |
| 10 | Amare Tezera Dessie | Pusan National University, Republic of Korea |
| 11 | Kyohyeon Gu | KAIST, Republic of Korea |
| 12 | Mustafa Hajij | University of San Francisco, United States |
| 13 | Jinyoung Heo | Kyungpook National University, Republic of Korea |
| 14 | Jaewoo Hwang | Kyungpook National University, Republic of Korea |
| 15 | Mee Seong Im | Johns Hopkins University, United States |
| 16 | Yeonhee Jang | Osaka Metropolitan University, Japan |
| 17 | Yewon Joung | Hanyang University, Republic of Korea |
| 18 | Ryoya Kai | Osaka Metropolitan University, Japan |
| 19 | Seiichi Kamada | The University of Osaka, Japan |
| 20 | Mikhail Khovanov | Johns Hopkins University, United States |
| 21 | Bogi Kim | Kyungpook National University, Republic of Korea |
| 22 | Byeorhi Kim | POSTECH, Republic of Korea |
| 23 | Geunyoung Kim | McMaster University, Canada |
| 24 | Hyoungjun Kim | Kyungpook National University, Republic of Korea |
| 25 | Jieon Kim | Pusan National University, Republic of Korea |
| 26 | Kee Taek Kim | KAIST, Republic of Korea |
| 27 | Miji Kim | Pusan National University, Republic of Korea |
| 28 | Youngju Kim | Kyungpook National University, Republic of Korea |
| 29 | Yoosik Kim | Pusan National University, Republic of Korea |
| 30 | Yumi Kim | Kyungpook National University, Republic of Korea |
| 31 | Hina Kitayama | Osaka Metropolitan University, Japan |
| 32 | Dongsoo Lee | KAIST, Republic of Korea |
| 33 | Hyungu Lee | Kyungpook National University, Republic of Korea |
| 34 | Sang Youl Lee | Pusan National University, Republic of Korea |
| 35 | Sangsoo Lee | Kyungpook National University, Republic of Korea |
| 36 | Meiling Li | Pusan National University, Republic of Korea |
| 37 | Ryohei Mashino | Osaka Metropolitan University, Japan |
| 38 | Haruko Matsuzawa | Osaka Metropolitan University, Japan |
| 39 | Thomas Mattman | California State University, Chico, United States |
| 40 | Ryosuke Miki | The University of Osaka, Japan |
| 41 | Fumika Mizoguchi | Osaka Metropolitan University, Japan |
| 42 | Junseok Moon | Kyungpook National University, Republic of Korea |
| 43 | Sam Nelson | Claremont McKenna College, United States |
| 44 | Jinseok Oh | Kyungpook National University, Republic of Korea |
| 45 | Joy Nana Okogun-Odompley | Pusan National University, Republic of Korea |
| 46 | Sanghoon Park | Pusan National University, Republic of Korea |
| 47 | Daesick Ryu | Kyungpook National University, Republic of Korea |
| 48 | Kazuki Sato | Osaka Metropolitan University, Japan |
| 49 | Junwoo Seo | Korea Science Academy of KAIST, Republic of Korea |
| 50 | Jinichiro Tanaka | Osaka Metropolitan University, Japan |
| 51 | Galmandakh Tsog-Ochir | Kyungpook National University, Republic of Korea |
| 52 | Haruchika Tsuno | The University of Osaka, Japan |
| 53 | Kodai Wada | Kobe University, Japan |
| 54 | Xiao Wang | Jilin University, China |
| 55 | Yuri Yamashita | Osaka Metropolitan University, Japan |
| 56 | Seung Yeop Yang | Kyungpook National University, Republic of Korea |
| 57 | Jumpei Yasuda | Osaka Metropolitan University, Japan |
| 58 | Hongdae Yun | Kyungpook National University, Republic of Korea |
| 59 | Yangyang Zhang | Osaka Metropolitan University, Japan |
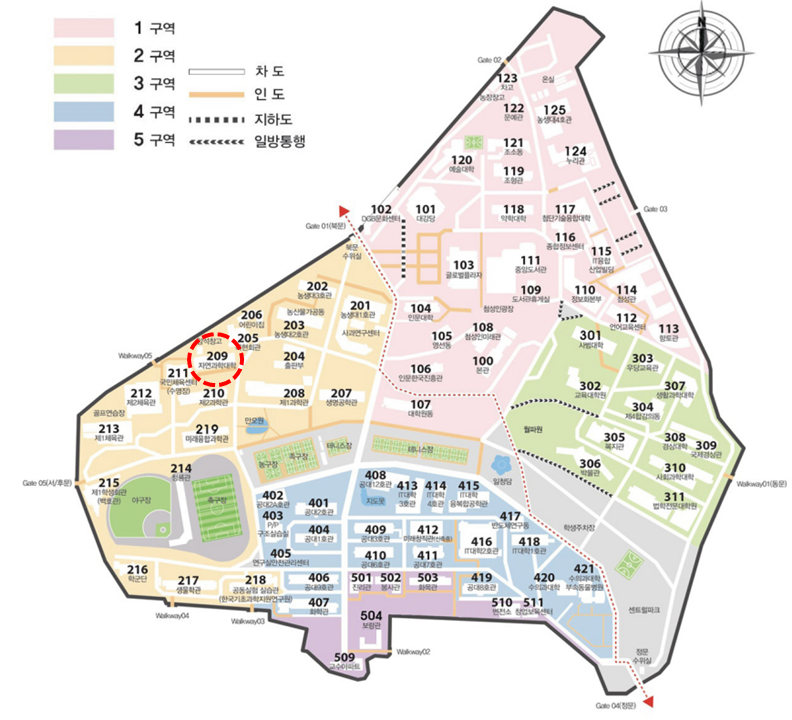
Venue
-
Conference Location
❍ Address(Department of Mathematics)
College of Natural Sciences Main Bldg.(#209), Kyungpook National University
80 Daehak-ro (Sangyeok-dong) 41566, Buk-gu, Daegu
❍ Lecture Rooms
Room 219
❍ Coffee Break Lounge
BK Lounge, 3rd Floor
-
How to Get to Daegu
(1) From Incheon International Airport (ICN) to Dongdaegu Station
❍ Option A: AREX + KTX (High-Speed Train)
■ From Incheon International Airport, take the Airport Railroad Express (AREX) to Seoul Station (~1 hour).
■ From Seoul Station, board a KTX to Dongdaegu Station (~1 hour 40 minutes).
※ Tickets can also be purchased at the ticket counters or ticket vending machines in both Incheon International Airport and Seoul Station. You can purchase tickets in advance as follows:
- AREX (Airport Railroad Express) tickets: Available at https://www.airportrailroad.com/co/main.do
- KTX (Korea Train Express) tickets: Available at https://www.korail.com/global/eng/main
❍ Option B: Direct Limousine Bus to Daegu
■ From Incheon International Airport Terminal 1 or 2, take a direct limousine bus to Dongdaegu Express Bus Terminal.
※ Buses depart every 30–40 minutes and go directly (with one short break-stop in the middle) to Dongdaegu Station. Depending on the traffic and the driver, it takes from 3.5 to 4.5 hours.
※ Tickets can be purchased at the airport limousine bus ticket counters on-site.
※ This option is convenient if you prefer a single-seat ride with no transfers, especially when traveling with large luggage. Tickets can be purchased at the airport ticket counters or online.
(2) From Gimhae International Airport (PUS) to Dongdaegu Station
❍ Option A: Metro + KTX
■ From the airport, take the Busan–Gimhae Light Rail Transit to Sasang Station.
■ Transfer to Busan Metro Line 2 and travel to Busan Station.
■ From Busan Station, take the KTX to Dongdaegu Station.
❍ Option B: Direct Express Bus from Gimhae Airport
■ Direct buses to Dongdaegu Express Bus Terminal are available from Gimhae Airport or nearby Sasang Bus Terminal.
※ The trip takes approximately 1 hour 10 minutes, and buses depart every 30–60 minutes. -
Accommodations
(1) Inter-burgo Exco Hotel
❍ Address: 80 Yutongdanji-ro, Buk-gu, Daegu 41515, Republic of Korea
❍ Tel: +82-53-380-0114
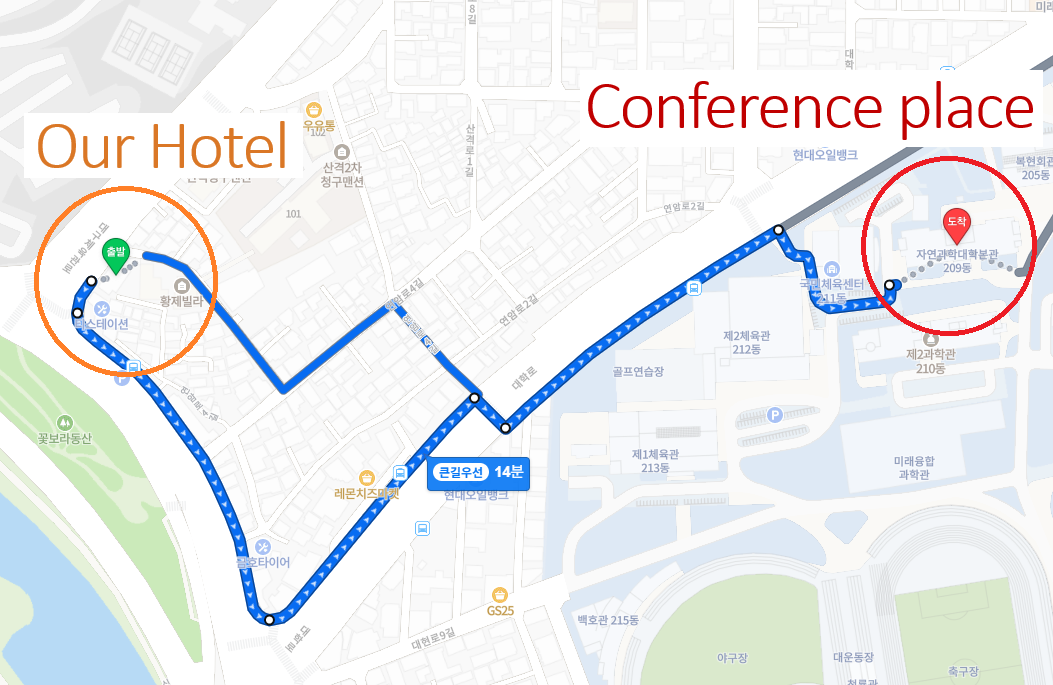
(2) Brown Dot Hotel, Kyungpook National Univ. Branch
○ Address: 2 Daegcheugkwan‑ro, Buk‑gu, Daegu, 41543, Republic of Korea
○ Tel: +82‑53‑267‑0111
○ Directions from your Hotel to Conference :
1. Exit the hotel and walk straight.
2. Turn left at the first corner, then left again at the next junction.
3. Cross the street, then turn left onto the road ahead.
4. Turn right at the next corner(Actually, it’s stairs.)
5. After climbing all the stairs, walk straight for a short distance, then turn left and continue a little further.
6. You’ll see the Mathematics Building entrance on your left—you’re there!
-
Meals and Banquets
All meals during the conference will be provided by the organizing committee. Below is the planned meal schedule:
❍ July 28 (Monday) – Welcome Dinner
• Dinner (starts at 19:00): Ashley Queen's Lotte Department Store Daegu Branch 9F, 161, Taepyeong-ro, Buk-gu, Daegu
❍ July 29 (Tuesday)
• Lunch (starts at 12:10): Bibimga, 2F Global Plaza, Kyungpook National University
• Dinner (starts at 18:30): Jangwon, 54, Sangyeok-ro 1-gil, Buk-gu, Daegu
❍ July 30 (Wednesday)
• Lunch (starts at 12:10): Bibimga, 2F Global Plaza, Kyungpook National University
• Banquet (starts at 18:30): Gonggan Sikdang, 59-5 Daeheon-ro 9-gil, Buk-gu, Daegu
❍ July 31 (Thursday)
• Lunch (starts at 13:10): Bibimga, 2F Global Plaza, Kyungpook National University
• Farewell Dinner (starts at 18:30): SKY17, 17F Global Plaza, Kyungpook National University -
Recommended Sightseeing in Daegu
Daegu offers a variety of attractions that combine natural beauty with cultural experiences. During your stay, you may wish to visit the following:
❍ Suseong Lake (Suseongmot)
A tranquil urban oasis featuring walking trails, paddle boats, and a nightly fountain show—a perfect spot for relaxing after conference sessions.
❍ Dongseongno & Kim Gwangseok-gil Street
A vibrant cultural area in downtown Daegu: Dongseongno offers lively nightlife and international dining, while nearby Kim Gwangseok-gil honors the beloved folk singer with murals, street performances, and artsy cafés
❍ E-World & Woobang 83 Tower
A family-friendly amusement park topped with the iconic 83 Tower. Ride the Ferris wheel, enjoy thrilling attractions, and ascend the tower for sweeping views of the city from the observation deck or the revolving restaurant
❍ Donghwasa Temple & Gatbawi—Palgongsan Mountain
Explore the serene Donghwasa Temple on the slopes of Palgongsan, then hike to (or take the cable car toward) the remarkable Gatbawi Buddha—a nationally recognized treasure dating back to the 9th century
